Technische Universität Wien
Orientation and Processing of Airborne Laser Scanning data
Department of Geodesy and Geoinformation - Research Groups Photogrammetry and Remote Sensing
Provides different line merging and topology correction tools for cleaning line networks derived via automatic edge detection.
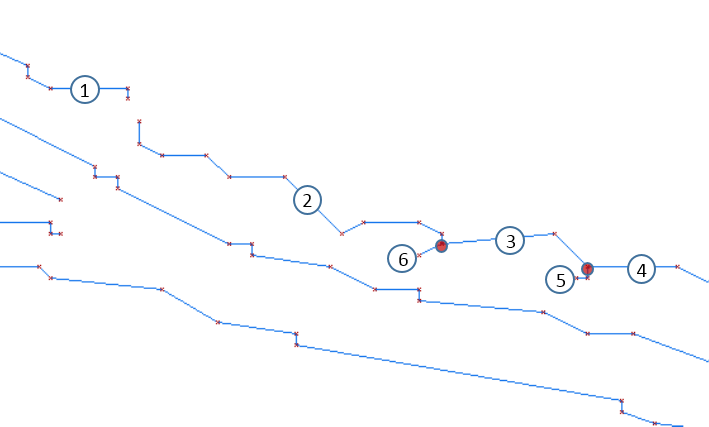
Many application require a continuous and topologically correct line network. Automatic line detection procedures (e.g. based on the Canny algorithm, cf. Module EdgeDetect) result in line networks which need post-processing for fulfilling the above aim of topological consistency and completeness. In the context of topographic mapping structure lines denoting surface slope discontinuities or even height jumps are of crucial importance. They can be regarded as the relevant linear features to portrait the landscape. Whereas full automation is hard to achieve for anthropologically shaped landscapes and manual editing might become necessary to achieve full completeness and correctness Module LineTopology aims at minimizing the manual editing effort by providing multiple line merging and topology correction strategies. Figure 1 shows vectorized line segments resulting from Canny edge detection highlighting the basic problems: (a) gaps in the line course and (b) line nodes/junctions
To overcome the above mentioned shortcomings Module LineTopology offers the following strategies (parameter method)
Module LineTopology tries to closing small gaps between individual line parts (snapRadius). As the reliability of automatically detected line paths tends to be poorest at the line ending, not only the very endpoints are considered as line connection candidate points but also points at the line end range (revertDist, revertIntervall). For merging two free ending lines the following issues need to be considered:
For merging two adjacent line endings the optimum line connection is found by analysing all candidate connections in the end range of both lines. For each connection the following parameters are checked:
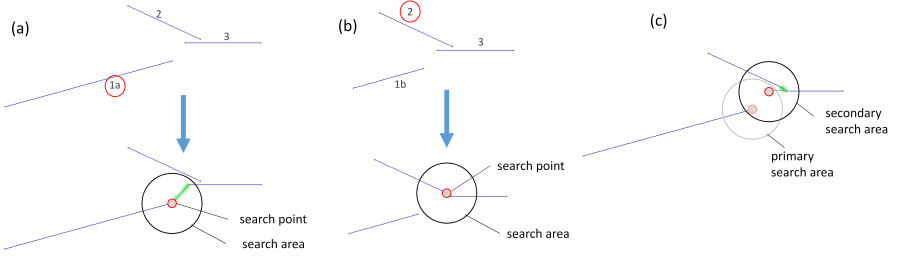
Each of the above mentioned parameters is scaled as an individual weight between 0 and 1 and the overall weight of a single connection candidate is obtained by multiplying all individual weights. The user can influence the rating by assigning scale factors for the individual weights (parameter group: weight factor options; dist, angle, revertDist, straightness, perpDist). Figure 2 shows an example where a small angular difference was favoured over a small connection-point-to-line-end-point (i.e. revert) distance.
If more than two lines are located within the line connection search area, the optimum line connection pair needs to be determined. As illustrated in Figure 3 a and b different line connections are found depending on the processing sequence. In Module LineTopology the lines are first ordered by descending length. The connecting line found for the longer line 1a in Figure 3a, however, is suboptimal as the connection between line 2 and 3 (Figure 3b) is favourable. Therefore the basic merging strategy outlined above is embedded in a generation based analysis. Starting with line 1b and the found connection candidate (line 3), the candidate selection is extended using line 3. Analysis of the end of line 3 reveals a better connection (to line 2) than was found before for line 1a. In general the described strategy results in globally optimal line connections. However, due to performance considerations the maximum number of search generations can be limited with parameter searchGeneration.
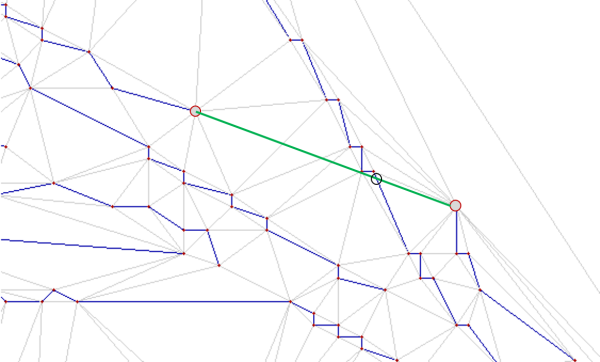
To avoid crossings within the line network introduced by establishing a new line connection, a triangular irregular network (TIN) is constructed from the initial line strings. Each line segment is hereby inserted as a constraint edge in a Delaunay triangulation. By default, a connection candidate is rejected if the connection intersects a contraint edge of the TIN (preventIntersection). Figure 4 shows an example; the green connection line candidate is rejected because it intersects the interjacent line.
The general idea of processing method longest is to establish those line connections which results in the longest continuous path. First, all lines are ordered by descending length. Starting with the longest line, all line parts sharing a common end point (line intersections) or even exhibiting a small gap are inserted into two directed graphs (one in forward and one in backward direction). Lines are recursively inserted into the graph if the gap distance (snapRadius) and the line progression direction (-opalsparam{maxAngleDev}) are within the acceptable limits. The search for additional connection candidates is then repeated at the end of each inserted line. Original (i.e. input) line strings are hereby inserted as edges and line connections as nodes into the graph. In case of adjacent lines (i.e. end point of 1st line = start point of 2nd line) an additional dot-shaped node is inserted. Finally the Dijkstra algorithm is used to find the shortest path connecting all nodes. For both graphs (forward and backward direction), the nodes featuring the longest path length are chosen and all lines on these specific paths are connected. Subsequently, all original line parts contributing to the described longest path line merge are removed from the line stack and processing is continued with the next longest line (part). The procedure is repeated until the line stack is empty or no more line connection are found. Figure 5 shows a practical example.
With processing method clean double lines or line segments can be automatically removed. Furthermore, erroneous line intersections are automatically detected and broken open by introducing a small gap (omitDist). Please note, intersections of two lines in a common node are accepted and, thus, the lines are not split up in this case.
The envisaged application of Module LineTopology is to post-process line vector data stemming from automatic edge detection, in particular with Module EdgeDetect and Module Vectorize. In this specific setup small gaps between otherwise continuous line paths, line crossings, and dangling line segments are likely. Whereas there is no one-for-all strategy yielding optimal results for every case, the following approaches have proven to be successful:
Usage of processing method clean is advisable after manually editing the line vector data to double check and (re)establish topological correctness of the line network.
The data used in the following example can be found in the $OPALS_ROOT/demo/ directory. As a prerequisite the data of (flyover.laz) are imported into an OPALS data manager, a DTM grid is calculated, the DTM slope map is calculated and processed with opalsEdgeDetect, and finally the resulting binary raster is vectorized:
A common routine to get a complete and topologically correct line network is to use the following three steps:
The processing in step 1 is done to establish line connections that result in long continuous paths.
In the second step the module tries to close small gaps between different lines depending on the specified snapRadius.
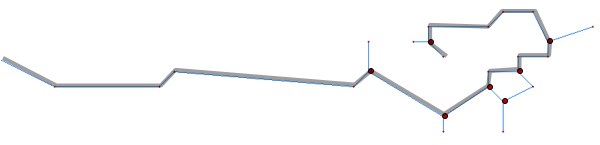
Step 3 again performs the longest path method to identify the longest possible continuous routes. The input DTM shading, all intermediate and final products of the above example are displayed in Figure 6.
G. Mandlburger, J. Otepka, C. Briese, W. Mücke, G. Summer, N. Pfeifer, S. Baltrusch, C. Dorn, H. Brockmann: Automatische Ableitung von Strukturlinien aus 3D-Punktwolken. in: "Dreiländertagung der SGPF, DGPF und OVG: Lösungen für eine Welt im Wandel", T. Kersten (ed.); Publikationen der Deutschen Gesellschaft für Photogrammetrie, Fernerkundung und Geoinformation e.V., Band 25 (2016), ISSN: 0942-2870; 131 - 142.
1.8.17