Module Simplify

Table of Contents

• Aim of module
• General description
• Parameter description
• Examples
• References

See also

opals::ISimplify

Aim of module

Analyses a regular or hybrid grid model and generates an approximating TIN surface based on a coarse-to-fine approach.

General description

Due to the high amount of data provided by ALS sensors, the simplification of surface grids (DTM, DSM...) derived from dense ALS point clouds is an important issue, above all for data delivery. To condense the data contained in high resolution ALS grids, it is necessary to analyze the surface and preserve all relevant surface features while, at the same time, generalize the surface as much as possible. Module Simplify uses a mesh refinement approach to iteratively refine an initial coarse grid.

The basic parameters for the data reduction are the input grid (parameter infile), a maximum height tolerance \(\Delta z_{max}\) (parameter maxTol) and a maximum planimetric point distance \(\Delta xy_{max}\) (parameter maxDist). The algorithm starts with an initial approximation of the input grid comprising a coarse regular grid (cell size=dxymax= \(\Delta_0\)) and all line information, which are triangulated using a constrained Delaunay triangulation. Each \(\Delta_0\)-cell is subsequently refined by iteratively inserting additional grid points until the height tolerance \(\Delta z_{max}\) is met. The general processing sequence is illustrated in Figure 1:

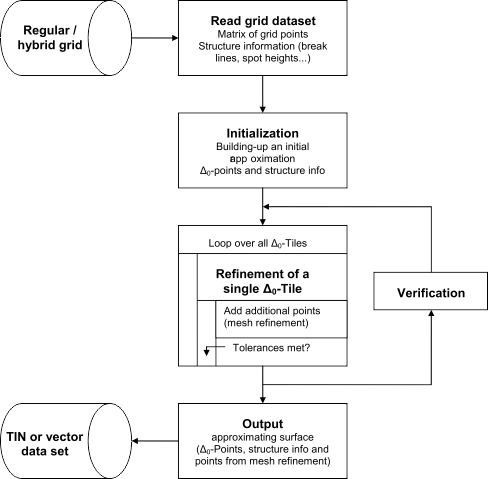
Fig.1: General surface simplification workflow

Within the refinement loop, additional vertices can either be inserted hierarchically or irregularly (parameter division). In case of hierarchical division, the grid cell is divided into four parts in each pass, if a single grid point within the regarded area exceeds the maximum tolerance \(\Delta z_{max}\) resulting in a quadtree-like data structure. By contrast only the grid point with the maximum deviation is inserted when using irregular division. Higher compression rates (up to 99% in flat areas) can be achieved with irregular point insertion, whereas the hierarchical mode is characterized by a more homogeneous data distribution. Figure 2 shows the different point distribution based on hierarchical and irregular division.

Fig.2: Point distribution with hierarchical (left) and irregular (right) division

Parameter description

-inFileinput grid model file

Type: opals::Path
Remarks: mandatory
The input grid model file is expected in aGDAL supported data format.

-outFileoutput file (simplified surface)

Type: opals::Path
Remarks: estimable
The simplified surface is stored as vector or TIN dataset depending on the output data format. Estimation rule: input file name + '_simpl' + <.ext>.Please note, that a correct representation of the approximated surface is ensured for TIN output only. In case of vector output, only the vertices and edges can be exported and, thus, reconstructing the surface from these points/lines may not lead to the same approximating surface and the adherence of the maximum height threshold can, therefore, not be assured.
Estimation rule: The current directory and the name (body) of the input file is used as file name basis. Additionally, the default extension of the output format is appended

-oFormatoutput TIN or vector file format

Type: opals::String
Remarks: estimable
Supported vector formats: WNP,BWNP,XYZ,BXYZ
Supported TIN formats: STL,REB,DXF,UCD,2DM,CityGrid XML,GPTIN
Estimation rule: The output format is estimated based on the extension of the output file (*.tif->STL, *.d45->REB, *.dxf->DXF ...).

-maxTolmaximum height tolerance

Type: double
Remarks: default=0.15
The simplified surface is constructed, so that the maximum height difference between the input grid and the simplified surface is less than maxTol

-maxDistmaximum point distance

Type: double
Remarks: default=16
Indicates the maximum point distance within the approximated surface

-divisioncell division mode

Type: opals::DivisionMode
Remarks: default=irregular

Possible values:  
  irregular ...... free division division of cells
  hierarchical ... quad-tree division of cells 

Hierarchical division: grid cell is divided into four parts resulting in a quadtree-like data structure. Irregular division: only the grid point with the maximum deviation is inserted. Higher compression rates can be achieved with irregular point insertion, whereas the hierarchical mode features a more homogeneous data distribution.

-lineVertexDistline vertex spacing

Type: double
Remarks: estimable
In case the input terrain model includes line information (structure lines and/or border lines, a regular vertex spacing along the lines is often useful to avoid thin triangles and/or long triangle edges.
Estimation rule: If not explicitly specified, 4*DTM-grid-width is used as line densification interval. Setting line vertex distance to zero suppresses line densification at all.

-lineBufferDistline buffer distance

Type: double
Remarks: estimable
The line buffer distance denotes the width of a band around structure lines of the DTM. Within the band all eventual grid points are removed to avoid small and odd-shaped triangles.
Estimation rule: If not explicitly specified 2*DTM-grid-width is used as buffer distance.

Examples

As a prerequisite for the subsequent examples, generate a digital surface model of the dataset strip21.laz (located in $OPALS_ROOT/demo/) by executing the following commands:

opalsImport -inFile strip21.laz
opalsGrid -inFile strip21.odm -outFile strip21.tif -gridSize 1 -interpolation movingPlanes

To obtain a simplified surface model with a maximum height tolerance of 25cm compared to the original DEM, type:

opalsSimplify -inFile strip21.tif -outFile strip21_red_25cm.stl -maxTol 0.25 -maxDist 16

A perspective view of the resulting TIN is shown in Figure 3.

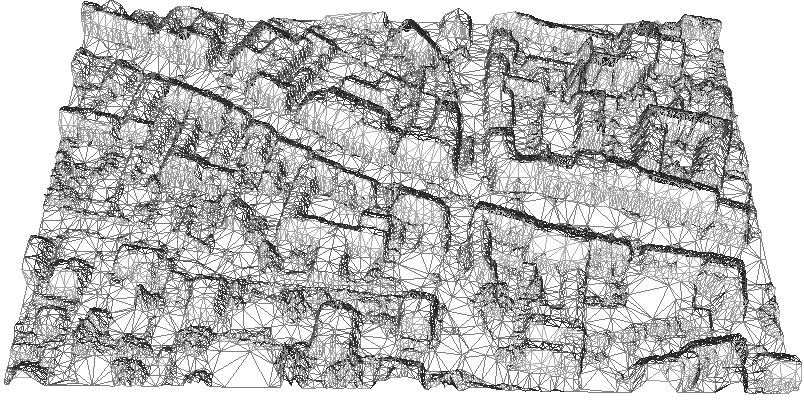
Fig.3: Simplified DEM TIN (max.tol.=25cm)

References

Mandlburger, G., Hauer, C., Höfle, B., Habersack, H. & Pfeifer, N., 2009: Optimisation of lidar derived terrain models for river flow modelling. Hydrology and Earth System Sciences, 13 (2009), S. 1453 - 1466.

Mandlburger, G. (2006). Topographische Modelle für Anwendungen in Hydraulik und Hydrologie. Ph. D. thesis, Vienna University of Technology