Technische Universität Wien
Orientation and Processing of Airborne Laser Scanning data
Department of Geodesy and Geoinformation - Research Groups Photogrammetry and Remote Sensing
Derives feature models (slope, curvature, roughness, etc.) from grid models based on the local grid neighbourhood defined by a kernel.
Apart from the terrain height, Digital Terrain Models allow the derivation of additional features based on the local grid neighbourhood. Important features are, for instance, the terrain slope and curvature. Although the most accurate results are obtained by deriving these features as a by-product of the surface interpolation using the original point cloud in Module Grid, there are a couple of advantages for deriving these features on raster basis:
The grid features are derived by taking all grid pixels into account within a certain kernel environment defined by its size (kernelSize, i.e. the kernel radius) and its shape (kernelShape, i.e.: square, circle, diamond). The following figure illustrates some standard cases:
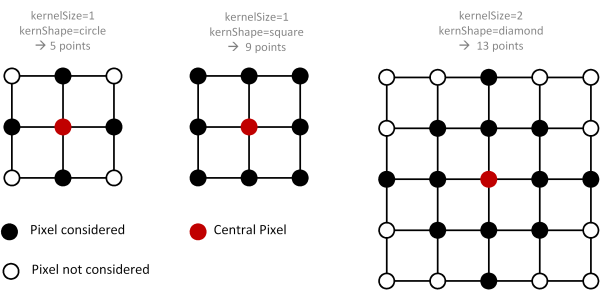
In general, the features are derived based on an appropriate underlying functional model. All slope related features, for instance, are calculated based on the best fitting plane defined by all valid grid points within the kernel. Curvature related features, in turn, are derived from a best fitting paraboloid. Multiple features can be calculated simultaneously simply be specifying a list of grid features (feature).
The following features are supported:
| Feature | Derived from | description |
|---|---|---|
| sigmaz | Plane | sigma z of grid post adjustment (i.e. std.dev. of the interpolated height) |
| sigma0 | Plane | sigma 0 of grid post adjustment (i.e. std.dev. of the unit weight observation) |
| slpPerc | Plane | steepest slope [%] |
| slpDeg | Plane | steepest slope [deg] |
| slpRad | Plane | steepest slope [rad] |
| exposRad | Plane | slope aspect [rad] (azimuth of steepest slope line, N=0, clockwise) |
| exposDeg | Plane | slope aspect [deg] (azimuth of steepest slope line, N=0, clockwise) |
| normalx | Plane | x-component of surface normal unit vector |
| normaly | Plane | y-component of surface normal unit vector |
| kmin | Paraboloid | minimum curvature [1/unit] |
| kmax | Paraboloid | maximum curvature |
| kmean | Paraboloid | mean curvature: kmean=(kmin+kmax)/2 |
| kgauss | Paraboloid | gaussian curvature: kgauss = kmin*kmax |
| kminDir | Paraboloid | direction (azimuth) of minimum curvature [rad] |
| kmaxDir | Paraboloid | direction (azimuth) of maximum curvature [rad] |
| absKmaxDir | Paraboloid | direction (azimuth) of maximum absolute curvature [rad] |
For each specified feature a separate grid file is calculated. The output grid file names (outFile) can either be specified explicitly, in which case a user-defined file name has to be specified for each feature. In case no or only file name is specified, unique file names are automatically created by adding the eature name as a postfix. The output grid files containing the feature rasters are created in GDAL supported format (oFormat). Please note that the feature grids are created in the same structure (resolution/extent) as the input DTM (inFile). Optional user defined limits can be specified to restrict the area of interest (limit). Please note that, irregular limits are automatically aligned to the grid structure of the input raster as re-sampling is strictly avoided.
Possible values: sigma0 ....... sigma 0 of grid post adjustment (i.e. std.dev. of the unit weight observation) slope ........ steepest slope [%] (deprecated: use slpPerc instead) slpPerc ...... steepest slope [%] slpDeg ....... steepest slope [deg] slpRad ....... steepest slope [rad] exposition ... slope aspect [rad] (deprecated: use expoRad instead) exposRad ..... slope aspect [rad] (azimuth of steepest slope) exposDeg ..... slope aspect [deg] (azimuth of steepest slope) normalx ...... x-component of surface normal unit vector normaly ...... y-component of surface normal unit vector kmin ......... minimum curvature kmax ......... maximum curvature kmean ........ mean curvature: kmean=(kmin+kmax)/2 kgauss ....... gaussian curvature: kgauss = kmin*kmax kminDir ...... Azimuth [rad] of minimum curvature kmaxDir ...... Azimuth [rad] of maximum curvature absKmaxDir ... Azimuth [rad] of maximum absolute curvature precision .... grid post precision (derived from sigmaz, pdens and slope)The grid feature models are created in the same format and structure as the basic (input) surface model are derived. Please note that if more than one output file is specified, the number of output file names must match the number of specified features
The following examples rely on the grid model albis.tif located in the $OPALS_ROOT/demo/ directory.
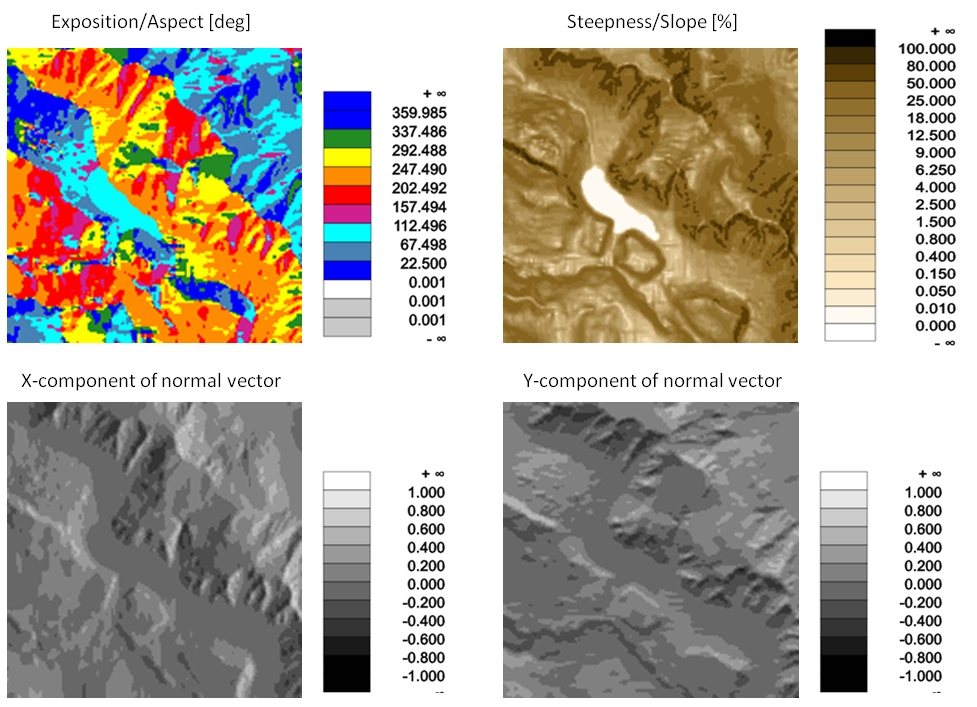
This first example demonstrates how to derive different slope feature grids (slope/steepness, exposition/aspect, x/y components of surface normal vector).
Since only the input file (albis.tif) and the feature list (slpPerc, exposRad, exposDeg, normalx, normal) where specified, the default kernel settings (kernel radius: 1, kernel shape: square) were used. Consequently, for each grid point a best fitting plane was estimated using the grid point and its eight neighbours. The requested features are all calculated from this (tilted) plane. The names of the output grid files composed automatically based on the input file name and using the standard feature postfixes. (albis_exposRad.tif, etc).
The visualizations shown in Figure 2 are obtained with the following commands:
In the second example different curvature rasters (minimum/maximum/mean/gaussian curvature) are derived. Hereby, a circular kernel shape and a kernel size (radius) of 2 pixels is used.
Figure 3 shows colour coded visualizations of the resulting curvature rasters which were derived using the following commands.
1.8.17