Derives a 2.5D digital elevation models (DEM) in regular grid structure using simple interpolation techniques.
Digital Surface Models (DSM) and Digital Terrain Models (DTM) are among the most important products derived from ALS point cloud data. DTM production based on ALS data is a complex task comprising (semi-)automatic modelling of structure lines, classifying the point cloud in terrain and off-terrain points and, finally, interpolating a smooth surface using high-level interpolation techniques like linear prediction or Kriging, respectively. In contrast, there are also a series of tasks within the ALS processing chain, which do not require the utmost quality concerning the geomorphological surface quality but, instead, shortest possible derivation times are crucial. This becomes especially true for the quality check of overlapping ALS strips (relative strip differences) based on distinct strip DSMs.
For this reason, Module Grid aims at deriving surface models in regular grid structure with maximum speed. To achieve high computation performance:
The ODM serves as data basis (parameter inFile) for the grid interpolation. Thus, the import of ALS point cloud data, stored in arbitrary data formats, is a prerequisite for Module Grid. For details concerning data import, please refer to Module Import. The interpolation results are stored as a regular grid file (parameter outFile) in a GDAL supported data format (parameter outformat). The internal processing is organised in patches (tiles), thus, maximum performance can be achieved for data formats supporting tile wise storage like, GeoTiff or SCOP.RDH. Sequential data formats (e.g. ArcInfo ASCII grid, DTED ...) can else be written directly by Module Grid, but probably with lower performance. The derived grid model is strictly stored in "pixel is point" interpretation, i.e. the grid values represent the interpolated heights at the pixel center. However, user defined limits (parameter limits) for the output grid model can either refer to the centers (=default) or corners of the outermost pixels (c.f. parameter limit description). For a more detailed discussion "grid versus raster" please refer to the glossary.
The following interpolation strategies (parameter interpolation) ordered by increasing processing time are offered:
The last four methods (moving average, moving planes, moving paraboloid, robust moving planes) require the specification of the number of neighbouring points considered for the interpolation of a single grid post (parameter neighbours). The results of the neighbour queries can be restricted to a maximum search radius around the grid point (parameter searchRadius), thus, enabling to reflect areas with sparse point density in the resulting grid as void pixels.
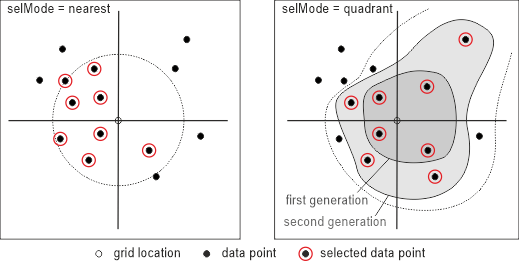
Furthermore, two different data selection strategies are offered: parameter selMode=nearest is the default mode representing the straight forward nearest neighbour query, whereas parameter selMode=quadrant yields a quadrant oriented data selection. In the latter case, the returned points are equally distributed among the four quadrants (NW, NE, SE, SW) around the (x,y) interpolation location (c.f. figure below), as long as, the number of neighbours is a multiple of four (4, 8, 12, ...). Hence, the first, second, third, etc. generation of quadrant neighbours are returned. If the number of neighbours has a remainder to 4, these "extra points" are also selected from different quadrants based on the distance criterion. In cases with empty (or inappropriate covered) quadrants this selection method only returns fully covered generation of quadrant neighbours, plus the appropriate number of extra points. E.g. if there are no points in two quadrants this method will always return 2 points (from the covered quadrants) even with higher number of neighbours than two. Please note, that quadrant oriented data selection avoids grid extrapolation effects but slows down the performance. Alternatively, grid extrapolation effects can also be reduced by specifying a greater number of neighbouring points together with using the default selection mode (parameter selMode nearest), which often results in better computation performance.
As mentioned above, the primary aim of Module Grid is the derivation of surface grid models. In addition, additional feature models (parameter feature) can be derived simultaneously as some of them are side products of the grid interpolation and, thus, can be provided without loss of performance. The following additional features are supported:
By default, the additional features are stored as separate grid model files in identical grid structure and data format as the corresponding surface model. The file names are either constructed automatically, if only the name of the surface grid model file is defined, based on the definition of the respective global postfix parameters (postfix_sigma, postfix_pdens, postfix_excen, postfix_slpPerc, postfix_slpDeg, postfix_slpRad, postfix_exposRad, postfix_exposDeg, postfix_nx, postfix_ny, postfix_kmin, postfix_kmax, postfix_kmean, postfix_kgauss,), or individual output file names can be specified. In the latter case, the number of entered file names must correspond to the number of derived grid models (surface model + feature models). Additional feature models are especially useful for subsequent creation of grid masks using Module Algebra. If the boolean parameter multiband is set to true or 1, respectively, only a single raster file with multiple bands is created. The first band always contains the z/attribute-raster followed by the feature bands in the order specified by the user.
In general, each point of the point cloud has the same influence on the run of surface. However, sometimes it might be useful to give preference to certain points (e.g. points with higher amplitude/reflectance or points closer to the grid point). Individual point weights can be achieved by specifying a point weight function formula (weightFunc) as a string in generic filter syntax. Individual point weights are reasonable/supported for all k-nn based interpolators (e.g.: movingAverage, movingPlanes, movingParaboloid, robMovingmovingPlanes). The formula is evaluated for each of the k-nn
points and must return a value which is used as weight for the respective point observation. To define a point weight, the following elements can be used:
As a general rule, the formulas should be defined so that valid weights can be computed for each k-nn point. A grid point will automatically be set to void (no data) if the weight function cannot be calculated for a single point of the k-nn set. The most frequent causes for numeric problems are divisions by zero (e.g. distance in the denominator) which can often be avoided by using a proper epsilon. For Inverse Distance Weighing, for instance, predefined formulae are available (idw1, idw2, idw:n, c.f. parameter description below for details).
Please note, that the outlier classification procedure within the moving planes estimation relies on the individual point weights and, thus, the rejection level can be controlled by assigning global or individual point weights. It is good practice to use the height variance (varZ=sqr(sigmaZ)) of a point as the basis for the weight calculation, with w = 1 / varZ.
Possible values: snap .................... simple 'snap-height-of-nearest-data-point' interpolation nearestNeighbour ........ nearest neighbour interpolation delaunayTriangulation ... Delaunay triangulation interpolation movingAverage ........... moving average interpolation (=moving horizontal plane) movingPlanes ............ moving (tilted) plane interpolation robMovingPlanes ......... robust moving (tilted) plane interpolation movingParaboloid ........ moving circular, elliptic or hyperbolic paraboloid kriging ................. kriging interpolationThe grid interpolation methods are ordered by quality. Higher-quality surfaces can be achieved using the latter methods but, in turn, the processing performance decreases.
Possible values: nearest .... pure nearest neighbour (nn) selection quadrant ... quadrant-wise nn selection, ie. nn per quadrant, then 2nd nn per quadrant, ...Please note that quadrant wise data selection on the one hand reduces extrapolation effects, but on the other hand decreases the processing performance
Possible values: sigmaz ......... sigma z of grid post adjustment (i.e. std.dev. of the interpolated height) sigma0 ......... sigma 0 of grid post adjustment (i.e. std.dev. of the unit weight observation) pdens .......... point density estimate pcount ......... number of points used for interpolation of grid point excentricity ... distance between grid points - c.o.g. of data points slope .......... steepest slope [%] (deprecated: use slpPerc instead) slpPerc ........ steepest slope [%] slpDeg ......... steepest slope [deg] slpRad ......... steepest slope [rad] exposition ..... slope aspect [rad] (deprecated: use expoRad instead) exposRad ....... slope aspect [rad] (azimuth of steepest slope) exposDeg ....... slope aspect [deg] (azimuth of steepest slope) normalx ........ x-component of surface normal unit vector normaly ........ y-component of surface normal unit vector kmin ........... minimum curvature kmax ........... maximum curvature kmean .......... mean curvature: kmean=(kmin+kmax)/2 kgauss ......... gaussian curvature: kgauss = kmin*kmax kminDir ........ Azimuth [rad] of minimum curvature kmaxDir ........ Azimuth [rad] of maximum curvature absKmaxDir ..... Azimuth [rad] of maximum absolute curvature precision ...... grid post precision (derived from sigmaz, pdens and slope)If one or more features are specified, additional grid models in the same format and structure as the basic surface model are derived. Please note that if more than one output file is specified, the number of output file names must match the number of specified features: nr. outFile = nr. feat. + 1
The data used in the following examples can be found in the $OPALS_ROOT/demo/ directory. As the derivation of (surface) grid model relies on the ODM, the respective point cloud data has to be imported. The datasets fullwave.fwf and fullwave2.fwf containing full waveform ALS point data (x, y, z, gps time, amplitude, echo width, echo nr, echo qualifier) of a wooded area are used. The following pre-processing steps are required:
In the first example only the mandatory parameter (inFile) is specified. Thus, the command is very short and simple:
It produces the grid file fullwave_z.tif in the default GeoTiff file format. The grid extensions are determined from the bounding box of the entire ODM point data set. The simple snap grid interpolation is used, thus a poor quality surface is derived. The grid size was not specified and, therefore, set to 1m.
In the second example some of the optional parameters are defined.
opalsGrid is called twice in this example. Two 0.5m grids are derived using moving planes interpolation. Whereas in the first case, the output is written in GeoTiff file format to file all.tif, an ArcInfo ASCII grid file (all.asc) is created in the case. In both examples the output format is estimated based on output file extension (*.tif->GeoTiff, *.asc->AAIGrid). The ASCII grid file contains a 6 line header containing the following georeferencing information of the grid file.
We see, that a grid with 361 columns and 201 lines was created. Please note that the coordinates of the lower left grid corner (XLLCORNER/YLLCORNER) do not coincide with the 0.5m grid lines, but are shifted about half a pixel. This is an indication for the 'pixel-is-point' interpretation. Since XLLCORNER/YLLCORNER denote the coordinates of the lower left pixel corner, the centers of the pixel coincide exactly with the 0.5m grid lines, for which locations the grid values have been derived.
The following figure shows the 'raw' grid file all.tif (as displayed by IrfanView) and a color coded variant using the default color palette of Module ZColor :

In the following example a filter is utilised to extract the first and last echoes from the ODM separately:
This produces the following output (again color coded using the standard color palette):

It can clearly be seen, that the right grid computed from the last echoes is much smoother than the one derived from the first echoes, as the first echoes contain all the reflections from the vegetation.
As before, this example uses a filter to restrict the point set considered for model interpolation. In addition to the last echo filter, a generic attribute filter is used to select all points with an echo width less than 4.5ns.
Please note, that quoting the filter string is strictly necessary in this case due to the embedded blanks and special characters. It is recommended always to quote complex filter strings. For more detailed information about pre-selecting data please refer to the Filter manual.
Based on Example 4, this example shows how to use individual point weights based on the echo intensity (approximated as the product of amplitude and echo width). The higher the intensity the more influence the point should have on the course of the surface.
Besides attributes, the 2D distances from the k-nn points to the grid point can be used to calculate the point weigth. This is commonly referred to as Inverse Distance Weighting (IDW) and the reciprocal of the squared distances (1/d^2) is often used as point weight. Based on the build in SqrDist2D fcuntion this can be formulated as:
Please note, that the grid point is accessed as n[0] and the k-nn point as n[1]. The above formula results in a divisions by zero if a data point is planimetrically coinciding with a data point. In fact, the fullwave.fwf dataset contains one last echo at round meter coordinates.
Consequently, the weight function gets infinite when calculated for the grid locations...
... resulting in the following warning message:
This could be avoided by using an appropriate small epsilon value to secure that the denominator is grater than zero. In the special case of Inverse Distance Weighting predefined formulae are available. The proper replacement for the above weight function based on squared distances is IDW2.
Example 6 demonstrates the use of the robust moving plane interpolator, Again, weight functions are used in this example to control the outlier detection. In contrast to example 5, were individual point weights were calculated provided based on the intensity or the location of a point w.r.t the grid point, a mean estimated height accuracy is applied to all points. However, the robust plane estimation is executed twice with different point weights (-weightFunc 1 or -weightFung 25) to demonstrate the effect of more conservative or more progressive outlier removal on the resulting grid (c.f. Fig. 4)
Setting the point weight value to 1 or 25, respectively, corresponds to an estimated a-priori sigmaZ of 1m/0.2m (weight=1/sigmaZ**2). In the latter case (w=25), more points are detected as outliers, as the expected height precision is smaller (Fig. 4). The respective visualizations can be produced with the following commands:

Example 7 shows the usage of multiband. Multiband is a boolean parameter. When set to true (1), each feature is stored in the corresponding band of a single raster file.
The example creates a single output file fwf_multiband.tif containing four bands. The first band is the z raster, and the second band includes the sigma0 feature, the third one slpPerc and the last one the exposRad feature.