Provides a generic raster algebra calculator featuring mathematical, statistical and conditional operators.
Module Algebra is a powerful tool as it allows the combination of multiple input grid datasets, each potentiallz containing multiple bands, by means of a user defined algebraic formula. Basically, It can be used either as a selector, as a calculator or, in all generality, as a mixture of both. Module Algebra can be applied to derive, e.g.:
In general, the output grid (parameter outFile) is derived by applying an algebraic formula (parameter formula) combining the values of one ore more input grid models (parameter inFile). The input grids may contain one or more raster bands. A mixture of single- and multiband input is explicitely allowed. The formula can either be specified as a generic filter or in python syntax. In the latter case the python interpreter is used evaluate the formula.
By default, the output grid is created with the same pixel size as the first input grid, but an arbitrary pixel size can be specified using parameter gridSize. The extents of the resulting grid can either be specified by the user (parameter limit (left,lower,right,upper)) or they are calculated from of the outermost pixel centers of all input grid datasets involved. If no user defined limits are specified, either the common area (parameter limit intersect), the overall area (parameter limit union) or the extents of the i'th dataset (parameter limit dataset:i) are applied (c.f. section Parameter description for more details).
Module Algebra can deal with non-coinciding grid/raster models simultaneously. If necessary, the input grids/rasters are re-sampled according to the output grid structure prior to evaluating the formula (parameter resampling). To strictly avoid resampling, please specify resampling=never. This would lead to a program termination if any of the contributing input grid files would require resampling.
One of the core applications of Module Algebra is mosaicing. In this case multiple input datasets are spatially disjoint so that, in general, only a single raster value is available on a specific location (opposed to apllication scencarios with overlapping datasets). To speed up processing, parameter skipVoidAreas will pre-select all relevant input datasets when processing a specific local region (i.e. processing unit) and will exlude all datasets which do not overlap with this processing unit. Please note that in case skipVoidAreas is activated only the relevant subset of input rasters is available for the formula (cf details for details).
The following sections describe in detail how arbitrary formulae can be specified in Module Algebra using either Calculator or Python syntax.
This section describes how to define the algebraic formula using the calculator syntax. Calculators are a specific form of generic filters, which allow calculations, conditional expression, and assignments in addition to pure data sub-selection. Due to the better performance, it is highly recommended to use the calculator syntax whenever possible.
Within Module Algebra, the grid location and the grid values can be used accessed in the formula in the following way:
| Variable name | Description |
| x | x-coordinate (Easting) of the pixel location |
| y | y-coordinate (Northing) of the pixel location |
| r[ds_idx][b_idx|b_name] | pixel value with dataset index ds_idx and band index bd_idx (indices starting with 0), and band name b_name |
| invalid | general void indicator |
The specification of the 2nd (band) index is optional and defaults to band index 0. Thus r[0][0] is equivalent to r[0]. This simplifies processing of single-band grid/raster models (e.g. DTMs). In case of multi-band rasters, the bands can either be accessed via index (starting from 0) or via the respective band name. Named bands are commonplace, e.g., for RGB files, where the bands are typically named "red", "green", and "blue". The possibility to access bands via their names is specifically useful when combining datasets from different sources. E.g., for creating an RGB mosaic from multiple RGB as well as multi-spectral datasets, it is more convenient to use band names as the index identifying a certain color band may differ from dataset to dataset.
Using the syntax above we can now combine one ore more input grid values in an algebraic (calculator) expression to compute a scalar value representing the respective output grid value. The general assignment syntax is:
band denotes the index or name of the raster band and type its data type (uint8, int8, uint16, ..., float, double). Alpha-numeric band names can be written with or without quotes, i.e., [red] or ["red"]. Quoted numeric values are explicitly used as (string) band names (e.g., ["0815"]) whereas non-quoted numeric values are used as band index (e.g., [0]). Both band names and types are optional. A default data type can be set via the global parameter data_type_grid. 32-bit float ((float or float32, respectively) is used if the data type is neither explicitely specified in the band assignment formula nor set via data_type_grid. Multiple bands can be calculated in a single call by separating the individual assignments with semicolons:
Please note that in case band names (and types) are omitted, the bands appear in the output file exactly in the same order as specified in the formula. In order to maintain compatibility with provious versions of Module Algebra, a single non-assignment statement as last statement of the formula string is permitted. Thus, the following statement is valid:
The above example results in a 3-band output raster although only 2 assignments are present. Assuming a single input dataset with a single band named "grad" (gradient raster), an output slope raster in % can be calculated as follows:
The prior three and the latter two statements are equivalent. Whereas the prior three statements use explicit naming of the output band, an unnamed band is produced in the latter two staments. The shortest possible syntax (omitting the band index) is:
In the above formula only a single input dataset is required, accessed by r[0]. In general, the datasets are strictely accessed by their index starting form 0, whereas the bands can either be accessed by name or index as explained above. The result of the expression (i.e. a scalar value) is assigned to the corresponding output grid cell.
It is recommended to use named bands as this facilitates interpretation of the dataset contents. Band names are consequently reported in all OPALS related log files. However, for the sake of brevity, band names and types are omitted in the following examples and the double indexed multi-band syantax is only used when necessary.
Another simple example is to subtract two input grids:
In this case, the difference is returned for all those pixels where both r[0] and r[1] exist. If either of the operands is invalid (i.e. nodata) the resulting output pixel will be invalid (nodata) as the expression cannot be evaluated correctly.
A typical application of Module Algebra is the derivation of (binary) grid masks. In this case either 0 or 1 is returned depending on a certain condition. Conditions can be specified in calculator syntax using the ternary operator:
In the above example, first the condition (r[0]*r[1]<1.0) is evaluated and depending on the binary result of the conditional expression 0 or 1, respectively, is returned as result of the entire formula. Please note that if one of the operands in the above condition does not exist, the entire condition evaluates to false, i.e. the else branch of the ternary operator is returned.
Within conditional expressions it is often desired to check both existence and value of certain pixels. Consider a formula returning the ratio between two grids:
For this formula we might want to check, if the grid value of the second input grid (r[1]) exists and is not equal to zero (otherwise the division will fail). Generic filters allow to query the existence of grid values by internally comparing the actual grid value with the grids (inherent) nodata value. For the example at hand we can simply write:
Please note the following details:
r[1] checks the existence of the grid value; i.e, the grid contains a valid value at the respective location.r[1]) and not-equal-zero (r[1]!=0) checks are concatenated with a logical "and" (&&)invalid is returned if the (entire) conditional expression is "false", which results in an invalid (nodata) output pixels.To support the creation of grid/raster mosaics, the generic filters provide statistical operators (min, max, mean, ...) for the entire stack of grid/raster values. Consider a set of stripwise DSMs (i.e. single-band grid models). In order to create a mosaic of all strip DSMs, we can simply write:
This returns the mean of all n valid input grids cells. Invalid grids cells (i.e., cell value = nodata value) are not considered for the statistical calculation. Expanding the previous single-band use case to mosaicing of multi-band RGB orthophoto tiles leads to the following syntax, this time using the full assignment syntax:
In this statemens (i) the output bands are explicitely named (as recommended in general) and (ii) the data type is set to 16-bit unsigned integer. The statement r[:][red] means "use the red band of all input datasets". The colon in the first (dataset) index is a special form of array slicing as, e.g. used in MATALB or Python. The general slicing syntax is: from:to, where from and to denote the optional start index (included, default=0) and end index (excluded, default:len+1). For calculating the mean of the red bands of the first four datasets, use either:
or:
By using negative indices (-1=last element, -2=one but the last element, ...), the same can be done for the last four datasets as:
Slicing is generally supported for both dataset and band indices. Thus, a simple panchromatic mosaic can be calculated via:
Slicing is neither meaningful nor supported for band names (e.g. r[:][red:blue]).
In order to increase the readability of the formula, intermediate calculation results can be stored in variables, which can immediatly be used in subsequent epressions and/or assignments. In the following example, a "raster cell density" is calculated by first defining the number of involved rasters, secondly counting the number of valid cells and, finally, returning the cell density.
In this example, only the latter statement follows the general rule for band assignments using square brackets. The first two statements, in turn, just store intermediate results, which are not considered for storage in the output raster.
Please note that, if no algebraic expression or band assignment is specified, a logical result is returned rather than the value. Thus, for a single-band input dataset
returns true (1) if r0 exists, otherwise false (0). Consequently, if we simply want to return the value of the first input grid, e.g. using Algebra as a raster format converter, we would have to write:
or
Generic filters are a very powerful tool providing a set of arithmetic, logical, conditional operators, and other features. As stated above, a detailed documentation can be found here.
Python syntax for specifying formulae is deprecated. While it was supported till OPALS version 2.3.2 for single-band rasters, Python syntax support is currently suspended and intended to be re-activated for upcoming versions including support of Python files (*.py) as input.
Delete from here ****************
An alternative way of specifying formulae in Module Algebra is to use Python syntax. In this case an internal Python interpreter is used to evaluate the formula. Although the performance is generally worse, the Python syntax offers more flexibility and should be used whenever the formula is too complex to be written in calculator syntax. The basic syntax of Python style formulae is:
where the return value represents the output grid value. Normally, the output grid value is a function of one or more input grid values. Let's assume that our input grid contains surface slope values (tangent of the steepest slope). In order to compute a grid containing the values of steepest slope in % we need to multiply the original slope values by 100. In this case, the formula reads:
where r[0] represents the grid value of the input grid. Of course, the combination formula can be much more complex, incorporating multiple grids, conditional statements and the like. A simple example based on two input grid models, which are used to create a grid mask (0|1) based on a certain threshold is:
The formula must be specified as a string in Python syntax. In fact, the Python interpreter is used to parse and evaluate the condition. Please refer to the Python documentation for a detailed description of the Python syntax. In the following, important information concerning the construction of formulas is summarized:
To access certain information of the considered grid models (pixel values, no data indicators, etc.), the following well-known variables are predefined:
| Variable name | Description |
| x | x-coordinate (Easting) of the pixel location |
| y | y-coordinate (Northing) of the pixel location |
| r[i] | pixel value of i-th input grid model (index starting with 0) |
| None | general void indicator (c.f. below for details). |
None is a constant representing a null-object in Python. It can be used to express empty or invalid objects of any type. In Module Algebra in particular, None is used to handle invalid input or output pixels. E.g., to verify if all input pixels are valid, one can write (for better readability in multi-line style):
The very same statement can be written in more compact format, without the None keyword:
Thus, in the first line the statement r[0]==None is equivalent to not r[0] (i.e. r[0] is invalid), and in the second line it is even allowed to skip the return value, as an empty return is equivalent to returning an empty object.
To combine the specific pixel values, a series of logical and mathematical operations are provided by Python. For a complete reference please refer to the Python language reference. The most important operations are listed below:
Boolean operations (or,and,not) ordered by ascending priority):
| Operation | Result |
| x or y | if x is false, then y, else x |
| x and y | if x is false, then x, else y |
| not x | if x is false, then True, else False |
Comparison operations:
| Operation | Meaning |
| < | strictly less than |
| <= | less than or equal |
| > | strictly greater than |
| >= | greater than or equal |
| == | equal |
| != | not equal |
| is | object identity |
| is not | negated object identity |
Built-in arithmetic operations:
| Operation | Result |
| x + y | sum of x and y |
| x - y | difference of x and y |
| x * y | product of x and y |
| x / y | quotient of x and y |
| x // y | (floored) quotient of x and y |
| x % y | remainder of x / y |
| -x | x negated |
| +x | x unchanged |
| abs(x) | absolute value or magnitude of x |
| int(x) | x converted to integer |
| long(x) | x converted to long integer |
| float(x) | x converted to floating point |
| complex(re,im) | a complex number with real part re, imaginary part im. im defaults to zero. |
| c.conjugate() | conjugate of the complex number c. (Identity on real numbers) |
| divmod(x, y) | the pair (x // y, x % y) |
| pow(x, y) | x to the power y |
| x ** y | x to the power y |
Apart from these basic operations, conditional statements are of crucial importance for the construction of complex formulas. Conditions can be specified either as single-line or as multi-line python statements:
Single-line conditional statement:
Multi-line conditional statement:
However, since the formula must be passed as a single string argument, line-breaks have to be entered via the special \n character sequence. The correct formula string corresponding to the example above is:
Since Python is an indent-oriented language (in opposition to languages using parentheses for grouping), the blank characters before the return statements are mandatory. The same applies to the \nelif... sequence, where no blank is allowed in order to ensure the correct indentation.
The formulas are not restricted to conditional statements, in fact, all control statements (for-loops, while-loops, etc.) are supported. The only preconditions are:
Delete to here ****************
Possible values: nearestNeighbour ... nearest neighbour bilinear ........... bi-linear interpolation bicubic ............ bi-cubic interpolation never .............. indicator avoiding resamplingMethod to be used for resampling the input grids to the specified grid structure of the output grid.
The data used in the subsequent examples are located in the $OPALS_ROOT/demo/ directory and the following preprocessing steps (data import and surface grid calculation) are required:
In the first example, the roofs of a digital surface model are extracted by applying a simple height threshold. All other values are set to void (no data).
Generic filter syntax:
Python syntax:
The output is written to a separate grid file in GeoTiff format (strip21_roofs[_py].tif) and a standard color coded visualization of it is shown in the following figure:
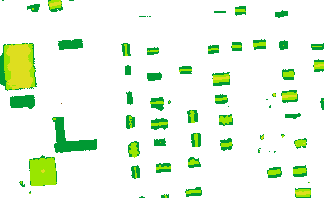
In this example, two grid models describing roughness (sigmaZ) and shadowing effects (excen), both by-products of the moving planes surface interpolation with /ref ModuleGrid, are used to create a binary grid mask (0..invalid,1..valid pixel).
Generic filter syntax:
Python syntax:
The very same condition can be written more compact as a single (binary) return statement:
Generic filter syntax:
Python syntax:
A simple way of creating a DTM mosaic based on multiple input grids (e.g. each grid covering a single map sheet) is by selecting the first valid grid value from the list of input grids for each grid position using Python's for .. in .. : statement:
Python syntax:
This commands takes three input grids (strip31.tif strip21.tif strip11.tif), calculates the xy-extents of the output grid as the union of all input datasets (-limit union) and, for each grid post, returns the first grid point with a valid height (-formula "... x:\n return x") within a loop over all input grids (-formula "for x in r[:]: ...").
To calculate a DTM mosaic based on the mean value of all valid pixels the following command in generic filter sysntax can be used:
The same result can be achieved using the wild card syntax for specifying the input files:
In the following example a (global) point density model is created based on strip-wise point density models. The strip-wise point density models can be created with the following command:
Now, we can calculate the global point density model as:
Generic filter syntax:
Python syntax:
Contrary to the previous example, all valid point densities values are summed up and the sum is returned (if the sum is greater 0).
Finally, opalsAlgebra is used for the derivation of a landscape dependent surface model as described in Hollaus et al (2010). Hereby, the single DSM pixels are either selected from a raster map containing the highest elevation within a cell (dsm_max.tif) or from a grid model calculated via moving planes interpolation (dsm_mp.tif) depending on a roughness map (dsm_mp_sigma0.tif, by-product of moving planes interpolation).
Generic filter syntax:
Python syntax:
Figure 2 shows hill shadings of all three DSM variants derived with the following commands:

In this example an orthophoto with RGB bands is splitted to sub images using limit parameter.
Generic filter syntax:
Python syntax:
Each sub-raster is stored with band names and data types which are defined in formula.
In the following example each band of an RGB orthophoto is seperately saved as single-band rasters.
Generic filter syntax:
Python syntax:
Following command generates an RGB mosaic image from 4 raster files.
Generic filter syntax:
Python syntax:
In this example selected bands from input rasters are organized and stored to a multiband single raster image.
Generic filter syntax:
Python syntax:
The following commands calculate VARI(Visible Atmospherically Resistant Index) and NDVI(Normalized Difference Vegetation Index) indices of input rasters. Then calculated indices are stored as a band in output raster.
Generic filter syntax:
Python syntax:
M. Hollaus, G. Mandlburger, N. Pfeifer, W. Mücke: Land cover dependent derivation of digital surface models from Airborne laser Scanning data; in: "IAPRS Volume XXXVIII Part 3A", (2010), ISSN: 168299750; 221 - 226.