- See also
- opals::IStatFilter
Aim of module
Performs statistical filtering of raster datasets with a sliding kernel of arbitrary shape and size.
General description
The Module StatFilter takes an input raster file (parameter inFile) and for each pixel calculates a statistical feature (parameter feature) by considering the neighbouring pixels in a user-defined kernel environment (parameter kernelShape, parameter kernelSize). The resulting output is again a raster (parameter outFile) in GDAL supported data format (parameter oFormat). The same statistical features as for Module Cell are provided, enabling low pass filtering (smoothing), boundary value extraction (min/max), roughness estimation, etc. The following features are provided:
-
min: lowest pixel within kernel area
-
max: highest pixel within kernel area
-
range: highest minus lowest attribute value
-
nmin: n-th lowest pixel
-
nmax: n-th highest pixel
-
mean: mean (average) of all pixels
-
median: median of all pixels
-
sum: sum of all pixels
-
rms: root mean square of all pixels
-
variance: (sample) variance of all pixels
-
stdDev: standard deviation of all pixels
-
stdDevMAD: robust standard deviation estimator computed from the median of absolute deviations from the median of all pixels
-
pcount: nr of valid (i.e. non-nodata) pixels
-
pdens: ratio of nr of valid (i.e. non-nodata) pixels to the nr of kernel pixels
-
quantile: p-quantile (p=0..1) of all kernel pixels
-
shannonEntropy: shannon entropy with specifiable bin width, measure of information content
-
quadraticEntropy: quadratic entropy with specifiable bin width, measure of information content
-
minority: class with the lowest frequency (based on a histogram of all pixels within kernel area. The bin width can be specified after a ':'. Default value is 1). This is especially useful for integer-typed rasters where the pixel values represent e.g. class identifiers.
-
majority: class with the highest frequency (as above).
Depending on the application different neighbourhoods may be required. The following kernel shapes are supported:
-
square: Chebyshev metrics
-
circle: Euclidian metrics
-
diamond: Manhattan metrics
Please note, that the kernel size is to be defined as a radius (in pixels) rather than as number of columns and lines. For a kernel radius of 4 (i.e. 9x9 kernel) the resulting kernels are shown in Figure 1.
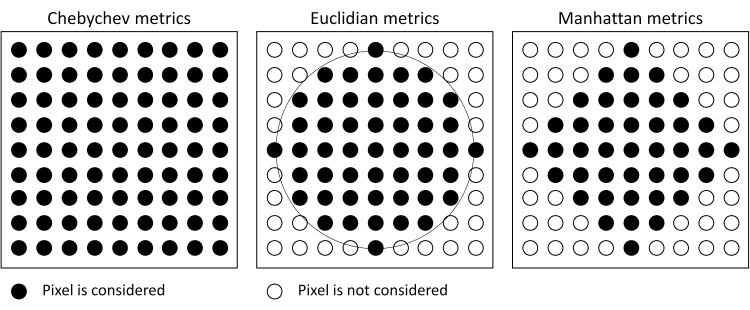
Figure 1: Square, circle and diamond kernels
By default, the input and output rasters have identical structure, i.e. for each input pixel a corresponding output pixel (containing the statistically filtered value) is calculated and stored. However, it is also possible to manipulate the output grid resolution (gridSize. The follwoing otions are provided:
-
gridSize=native: The output grid width corresponds to the input grid wdith
-
gridSize=halfKernel: The output grid width equals the kernel radius size (i.e. half kernel size)
-
gridSize=kernelSize: The output grid width equals the entire kernel size
Figure 2 illustrates the above mentioned resampling options:
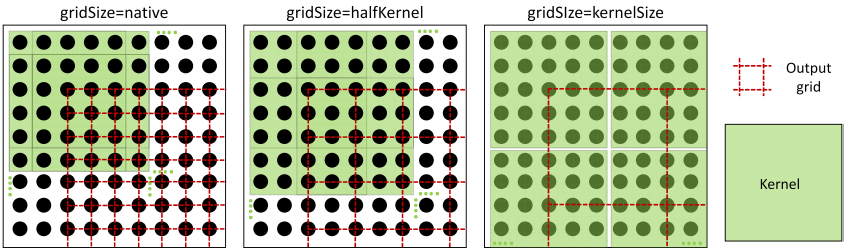
Figure 2: Left: no resampling), Middle: output grid width = kernel radius, Right: output grid width = kernel size
Furthermore, the output grid extents may be changed by specifying a user defined limit (limit). Please note, that uneven limits are automatically rounded to the next grid post position. Optionally, a no-data value representing data voids in the output raster can be specified (parameter noData).
Parameter description
-inFileinput raster file
Type:
opals::Path
Remarks: mandatory
Import raster image in GDAL supported format,
-outFileoutput raster file
Type:
opals::Path
Remarks: estimable
Path of filtered raster image file in GDAL supported format.
Estimation rule: The current directory and the name (body) of the input file are used as file name basis. Additionally, the postfix and the extension are constructed accoding to the specified and oFormat (e.g. '_min.tif').
-oFormatraster file format [GTiff,AAIGrid,SCOP,...]
Type:
opals::String
Remarks: estimable
Use GDAL driver names like GTiff, AAIGrid, USGSDEM, SCOP... .
Estimation rule: The output format is estimated based on the extension of the output file (*.tif->GTiff, *.dem->USGSDEM, *.dtm->SCOP...).
-featurestatistical feature
Type:
DM::StatFeature
Remarks: mandatory
A statistical feature of the set [min,max,diff,nmin:n,nmax:n,mean,median,sum,variance,rms,pdens,pcount,quantile:p,minority,majority,shanonEntropy, quadraticEntropy] is derived. For features nmin:n and nmax:n, n (>0) and for feature quantile p ([0,1]) must be specified
-kernelShapekernel shape
Type:
opals::KernelShape
Remarks: default=square
To select a predefined shape of the (binary) kernel matrix.
-kernelSizekernel size (radius of kernel in pixels)
Type: int32
Remarks: default=1
Kernel radius
-limit2D clipping window
Type:
opals::GridLimit
Remarks: optional
If no user defined limits are specified or -limit is even skipped, the entire xy-extents of the input raster model are used.
GridLimit: Defines xy-limits for output grid/raster datasets. The limit coordinates specified by left/lower/right/upper either refer to pixel centers (default) or corners, and may optionally get rounded to multiples of the grid size.
Syntax: ['center'|'corner']['round']['(' left lower right upper ')'] -noDatanodata value indicating void pixels
Type:
opals::NoDataType
Remarks: default=max
Value representing an undefined value in the output grid model.
NoDataType: Defines or disables (use 'none') the nodata value for the output raster. The nodata values can be a specific value or a type independent label, such as, 'min', 'max' and 'nan'. Those labels will be translate to values based on the raster band type. See the OPALS Docu (opals::NoDataType) for more Details.
Syntax: none | min | max | nan | <value> -procModereal or integer processing mode
Type:
opals::HistoMode
Remarks: default=automatic
For features aggregated into bins like minority and majority, the bin center is used as representative value. The same applies to procMode=integer, where the bin limits are shifted by half the bin size so that the corresponding integer value is located in the bin center. With procMode=real the bin limits are mutiples of the bin sizes, which is suitable for processing features of floating point (real) type. In automatic mode the module selects real or integer procMode based on the attribute type.
-gridSizeoutput grid size/resolution
Type:
opals::GridResolution
Remarks: default=native
By default, the output grid is calculated using the native input grid resolution. However, as the input pixels are used reduntantly for neigbouring output pixels in this case, a reduced resolution (half or entire kernel size) can be chosen. Especially for an output resolution corresponding to the kernelSize each input pixel is contributing to the resulting output grid one-time-only.
Examples
The following examples rely on the surface grids first.tif and last.tif derived from all first/last echoes of the dataset fullwave.fwf as described in Example 3: (Example 3) of module Module Grid.
Example 1:
By averaging all pixels within the kernel area, low pass filtering (i.e. smoothing) of raster datasets can be performed. The smoothing level can be controlled by the kernel size.
This corresponds to a kernel size of 3x3, 5x5, and 7x7 resulting in gradually higher smoothing rates. Please note, that since the kernel shape is not explicitly defined, the square kernel is used by default.
Example 2:
In this example, the min/max features are used to derive a DSM and DTM. In this example, the highest values of first-echo-surface model and the lowest values of the last-echo-surface model are filtered using circular kernel environment (euclidian metrics), resulting in a simple DSM and (very noisy!!) DTM. A hill shading of the two models is shown in Figure 3.

Figure 3: Left: DSM, max-filter based on first echoes, Right: DTM, min-filter based on last echoes
Example 3:
In this example the parameter gridSize=kernelSize is used to resample the output grid. The resulting grid has a grid width of 1.0 x 1.0m2 (i.e. native grid width of 0.5m x kernel radius of 2 pixels).
Example 4:
In this example the parameter gridSize is set to the entire size of the kernel resulting in a grid with a cell size of 2.5 x 2.5m2.
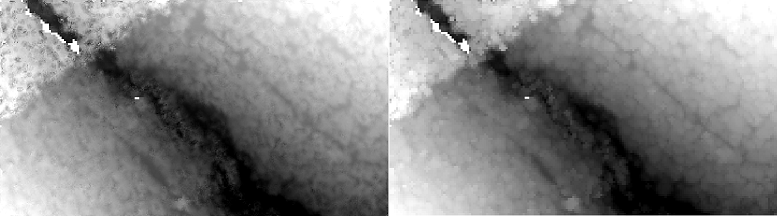
Figure 4: Left: DSM, max-filter based on first echoes, Right: Resampled DSM (grid size = half kernel size = 1m)
Example 5:
This example shows how to use the limit parameter. The result is sillustrated in Figure 4 below.
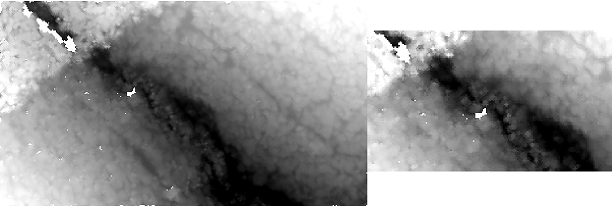
Figure 5: Left: DSM without limit, Right: DSM restricted to a user defined area-of-interest
- Author
- gm
- Date
- 23.06.2016




