Technische Universität Wien
Orientation and Processing of Airborne Laser Scanning data
Department of Geodesy and Geoinformation - Research Groups Photogrammetry and Remote Sensing
Derives and stores the 2D boundary polygon of a region covered by the point data of an ODM or the valid pixels of a raster.
Even though the (vague) outline or shape of a point set may seem visually intuitive and clear, it may be defined and computed in various ways. The respective approaches may be classified into methods directly acting on the vector data and others that use rasterized versions of the data (thus depending on respective cell sizes). Module Bounds provides several methods that operate on vector data and derive a 2-dimensional outline of the point set provided by an ODM or a grid/raster. This outline is represented as 1 strictly simple (i.e. non-self-intersecting) polygon that may be convex or concave, depending on the method.
By using the approximative mode a quick calculation based on the overview matrix (generated in Module Import) of the boundaries can be computed. The overview matrix has a maximum size of 400x400 and can be accessed without opening the ODM. Only the values on the edges are used for the triangulation, which further decreases the number of values to be considered for the calculation of the boundaries.
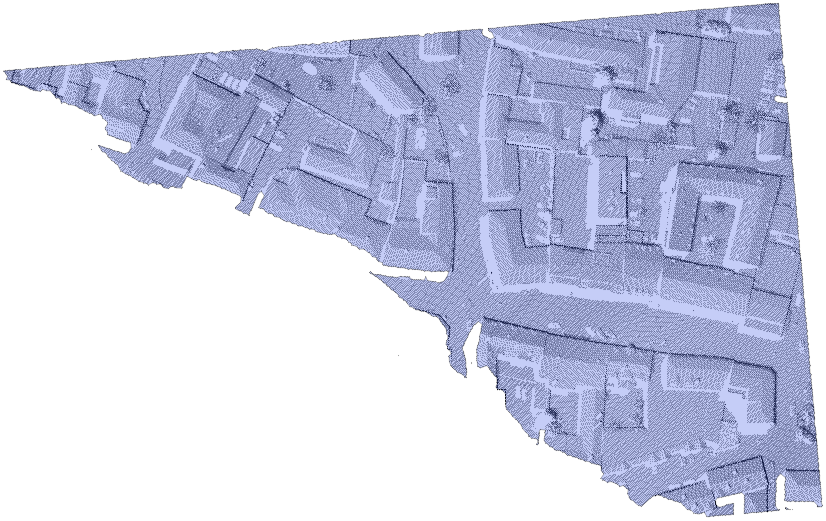
\(\alpha\)-shapes come close to what one would expect as a tight outline. \(\alpha\)-shapes are based on the triangulation of a point set. In regularized \(\alpha\)-shapes, as applied in Module Bounds, whole triangles together with their incident edges and vertices either belong to the shape or not, depending on the triangles' circumcircle radii, which must be smaller than the so-called \(\alpha\)-radius then. Therefore, the smaller the \(\alpha\)-radius, the fewer triangles form part of the \(\alpha\)-shape, and into the more connected components the \(\alpha\)-shape will be split. With increasing \(\alpha\)-radius, the \(\alpha\)-shape converges to the convex hull, constituting a single connected component only.
If the \(\alpha\)-radius is not specified, then Module Bounds uses the minimum \(\alpha\)-radius that makes all data points form part of the \(\alpha\)-shape and which yields a single connected component of \(\alpha\)-shape-triangles.
As the triangulation of large point sets is memory- and time-consuming, Module Bounds determines the coarse outline of data beforehand, and hence only triangulates the data within the outer regions. However, if point density varies largely within these regions, this approach may fail. In this case, a warning is emitted and the resulting \(\alpha\)-shape is the union of the computed \(\alpha\)-shape and the region omitted during triangulation. To avoid these failures, the parameter hollowingThresh may be set to a value larger than the number of data points: above this threshold, all points will be triangulated.
As a result, the outmost boundary of the \(\alpha\)-shape is used, being a possibly concave, but always strictly simple polygon.
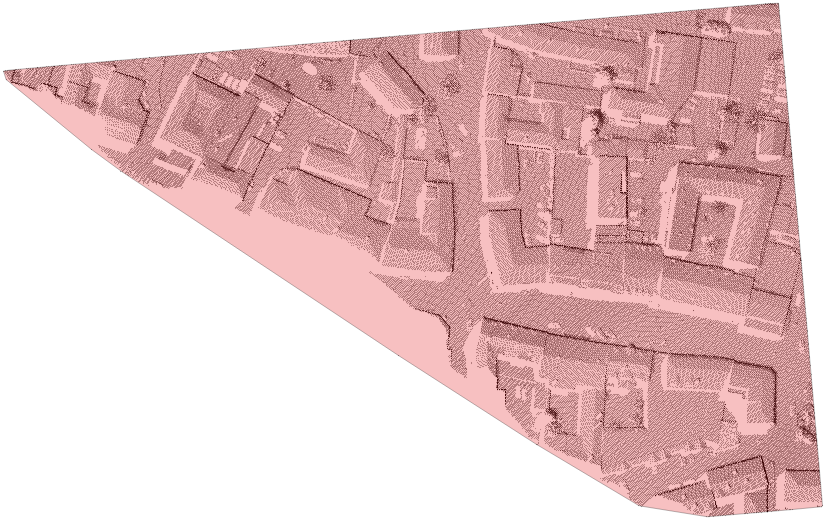
While the convex hull (generally) forms a coarser approximation to the data outline than \(\alpha\)-shapes do, this method is by far faster and features a much smaller memory footprint. As the name indicates, the resulting polygon is convex.
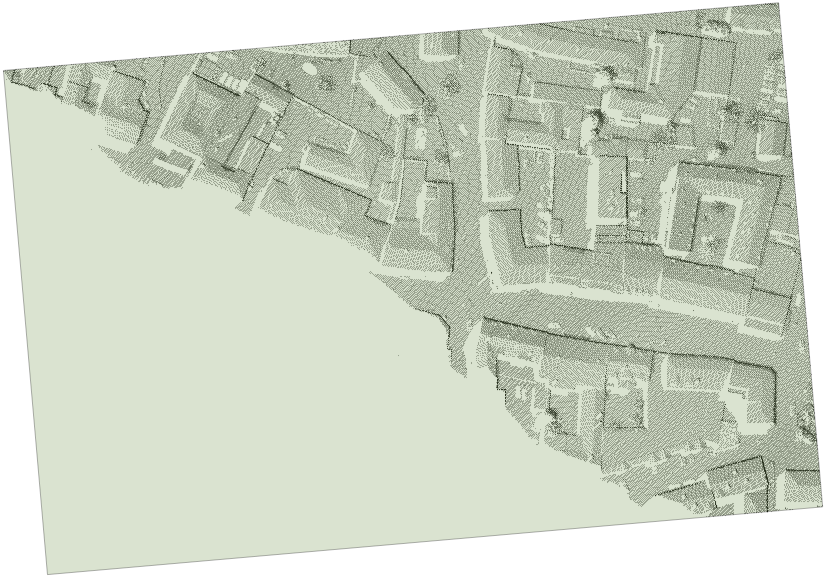
Based on the convex hull of the point set, this method derives the minimum rectangle that encloses all data points. This rectangle is oriented arbitrarily i.e. it is generally not axis-aligned.
Possible values: d2 ..... Search based on 2D coordinates (x and y) only d2_5 ... Search based on 3D coordinates but with different horizontal and vertical scalesCurrently, the 2d and the 2.5d calculation mode are supported. Whereas in 2d an average height for the alpha shape and the convex hull are extracted, in 2.5d mode the actual point heights are considered. Hence, the extracted polygons will run through the corresponding 3d points which might be relevant for some applications. On the other hand, the 2.5d algorithm requires more memory which might cause memory issues for huge data sets.
The data used in the following example are located in the directory $OPALS_ROOT/demo/. As the derivation of boundary lines relies on an ODM, the respective point cloud data has to be imported first. In this example, the dataset strip31.laz is used. To load the data into the ODM and rotate it counter-clockwise about the z-axis by 5°, change into the demo directory and type:
In this example, only the mandatory parameter (inFile) is specified. Thus, the command is simply:
It produces the boundary file strip31_bounds.shp, using 'convexHull' as the default boundsType. The output is the boundary line as shown in the figure of subsection Convex hull.
Whereas a 2D outline is suitable for most application, the module also supports a 2.5D computation using parameter calculationMode. Although both outline will have height information, in 2D calculation mode all points are set to an average height. In 2.5D mode the outline will pass through the boundary points in 3D as it can be seen in figure 4. The following example extracts two \(\alpha\)-shapes in 2D and 2.5D calculationMode.
By specifying approximative a quick calculation based on the overview matrix will be computed. The overview matrix can be accessed without opening the odm which leads to a faster computing time. For further optimisation only the values on the edges are used for the triangulation.
Tested on computer with an AMD Ryzen Threadripper 2920X 3.50 GHz 12-Core CPU and 32GB RAM the exact calculation was performed in 4 seconds while the approximate took less than 1 second.
1.8.17