Module EchoRatio

Table of Contents

• Aim of module
• General description
• Parameter description
• Examples
  • Example1
  • Example 2
• References

See also

opals::IEchoRatio

Aim of module

Derives and stores the echo ratio (ER) attribute for points of an OPALS data manager.

General description

The echo ratio (ER) is a measure for local transparency and roughness and is calculated in the 3D point cloud directly based on the ODM. The ER is derived for each laser point and is defined as follows:

echo ratio [%] = n_3D / n_2D * 100.0 (Equ. 1)

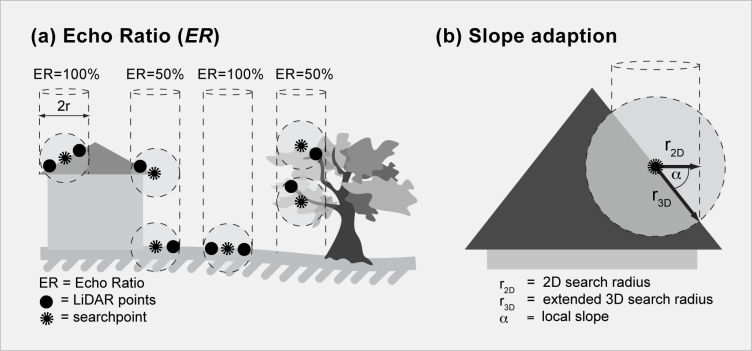
with n_3D <= n_2D, n_3D = no. of neighbors found in a fixed search distance measured in 3D (i.e. search sphere) and n_2D= no. of neighbors found in same distance measured in 2D (i.e. vertical search cylinder with infinite height). For impenetrable (flat) surfaces (bare ground) the echo ratio is (nearly) 100%, whereas the echo ratio decreases for penetrable surface parts (vegetation), since there are more points in a (vertical) search cylinder than there are points in a sphere with the same radius. With increasing surface slope (eg. roofs, walls), even if the surface is fully solid, the ER gradually decreases. To guarantee a high ER in steep impenetrable areas, the 3D search distance has to be extended considering the local surface slope. This is done by dividing the initial 3D distance by the cosine of the surface slope (r_3D=r_2D / cos(alpha)). Thus, the availability of local surface normal vectors is a prerequisite for deriving the slope adaptive echo ratio. See Module Normals for details concerning normals estimation. Figure 1 illustrates the difference between basic and slope adaptive echo ratio.

(a) Point cloud based calculation of ER for each laser point (i.e. search point) with example values for different landscape objects, and (b) slope adaption (i.e. extension of 3D search radius r3D) depending on the local surface slope

The main parameter of Module EchoRatio are the ODM file (parameter inFile) containing point coordinates (x,y,z) as well as the components of the local surface normal direction (nx, ny, nz, optional) for each laser point and the radius of the search cylinder / sphere (parameter searchRadius). A good estimate for the search distance is the double of the average laser point spacing. The echo ratio results are stored as /e EchoRatio in the ODM (see predefined attributes for details). Output in arbitrary formats is supported via the Module Export. By default, the slope adaptive echo ratio is derived for all ODM points containing valid normal vector information, whereas the basic echo ratio (according to Eq. 1) is calculated if no information about the local surface slope is available.

In general, the echo ratio derivation is carried out for all ODM points. However, one or two filter strings can be specified to select a subset of ODM data points (parameter filter). The first filter is interpreted as 'processing filter' and restricts the set of points for which the an echo ratio is to be calculated. The second filter serves as 'neighbourhood filter' and afftects the set of neighbouring points used in the echo ratio calculation. If only one (processing) filter is specified, the same filter is used as neighbourhood filter. If, however, the neighbourhood queries should consider all ODM points, the "Pass" filter or an empty filter (i.e. " " from within the commandline or "" in Python) must be used. For more detailed information about the filter string syntax, please refer to section Filters.

Parameter description

-inFileODM input file

Type: opals::Path
Remarks: mandatory
The ALS points, for which the echo ratio is to be derived, are read from an ODM file. The results (attribute echo ratio, ...) are stored back to the same ODM file as additional infos.

-searchRadiusmaximum search distance

Type: float
Remarks: default=1
For deriving the echo ratio of a single point, all points within a maximum 2D distance are queried and the number (n2d) is compared against the number of points in the respective 3D environment (n3d).

-ratioModeecho ratio calculation mode

Type: opals::EchoRatioMode
Remarks: default=slopeAdaptive
In case of ratioMode=slopeAdaptive, the slope adaptive echo ratio is derived for all points, for which the surface normals are stored in the ODM, otherwise the basic echo ratio (n3d/n2d*100) is calculated.

-filterfilter string

Type: opals::Vector<opals::String>
Remarks: optional
One or two filter strings in EBNF syntax (as described in section 'Filter syntax') can be passed to restrict the set of input points. The first filter specifies for which points an attribute should be calculated (if not specified, attribute calculation is carried our for all ODM points). The second filter defines which points are used for the neighbourhood query.

-maxSigmamaximum allowed sigma of plane fitting

Type: float
Remarks: default=0.3
This parameter is required when using the slope adaptive echo ratio.No slope adaptive echo ratio is derived for points having a plane fitting sigma higher than the value specified: instead the normal echo ratio is calculated.

Examples

The data used in the following example are located in the $OPALS_ROOT/demo/ directory. As a prerequisite, a dataset (strip21.laz) is imported and the surface normals using the following commands:

opalsImport -inFile strip21.laz
opalsNormals -inFile strip21.odm -neighbour 5 -searchRadius 2

Example1

On the basis of the resulting ODM (containing the laser points surface normal directions as additional info), the (slope adaptive) echo ratio is calculated, and the results are rasterized and visualized using a greytone colour palette:

opalsEchoRatio -inFile strip21.odm -searchRadius 2 -ratioMode slopeAdapt
opalsGrid -inFile strip21.odm -outFile ER.tif -inter movingPlanes -attribute EchoRatio -grids 0.5
opalsZColor -inFile ER.tif -outFile ER_image.tif -palFile greyPal.xml -nClasses 255

The resulting image ER_image.tif is shown in the follwoing figure:

Echo ratio image

Example 2

In this example, the use of two filter strings (processing filter and neighbourhood filter) is explained which is useful for speeding up processing by only calculating the echo ratio for a subset of the point. First, a DSM is calculated using the maximum elevation in 2m grid cell and the respective grid points are imported into a new ODM and marked with a flag and the ODM containing the laser points and normals are imported into this new ODM. Thereafter, the echo ratio is calculated only for the DSM points using only the laser points for the ER calculation.

  opalsCell -inFile strip21.odm -outFile dsm.tif -cellSize 1 -feature max
opalsImport -inFile dsm.tif -iFormat GTiff -outFile strip21_2.odm -filter "generic[_dsmPoint(bool)=true]"
opalsImport -inFile strip21_2.odm strip21.odm -outFile strip21_2.odm -filter "generic[EchoRatio=invalid]"
  opalsEchoRatio -inFile strip21_2.odm -searchRadius 2 -ratioMode slopeAdapt -filter "generic[_dsmPoint]"  "generic[not _dsmPoint]"

References

Höfle, B., Mücke, W., Dutter, M., Rutzinger, M. and Dorninger, P.

1. Detection of building regions using airborne LiDAR - A new combination of raster and point cloud based GIS methods, Angewandte Geoinformatik 2009, Beiträge zum 21. AGIT-Symposium Salzburg 2009.