Technische Universität Wien
Orientation and Processing of Airborne Laser Scanning data
Department of Geodesy and Geoinformation - Research Groups Photogrammetry and Remote Sensing
Estimates local surface normal vectors for each point of a specific point cloud (ODM).
Estimation of local plane information on a point basis is useful (or even necessary) for different tasks. Parameters that are derived by opalsNormal can be used to compute local slope and exposure values, roughness measures, values describing the point distribution and are input for other OPALS modules (e.g. opalsEchoRatio).
The module attaches the computed information to the input OPALS Data Manager (ODM). Different neighbour selection strategies, different plane estimation methods but also a very flexible way to process only a subset of input points are provided. Additionally it is possible to define the level of meta information that are stored with each point. Depending on the subsequent task appropriate parameter have to be set.
Currently three different normal estimator (see parameter normalsAlg ) are provided which can be mainly differentiate by their degree of robustness. simplePlane is a standard least-squares plane adjustment offering no blunder detection (fastest method). Hence, it should be used if the normal quality is of minor concern or the focus is set on a simple roughness detection strategy (non-planar region will lead to a higher sigma0 of the adjustment). robustPlane detects blunders using observation weighting based on their residual. After convergence all blunder are eliminated and a final adjustment, using equally weighted observations, is performed. The robust fmcd (Fast Minimum Covariance Determinant) estimator uses an additional inverse distance weighting strategy for better approximation of the local point environment. This complex estimation method is appropriate for very dense and very inhomogeneous point distributions.
If a robust estimator is selected, the number of neighbours (see parameter neighbours) should be clearly increased (>10). To reduce extrapolation effects it is possible to make a quadrant (or octant) orientated neighbbour selection. For more details on the quadrant selection strategie see section data selection strategies. Additionally it should be mentoined that the searchMode and selMode parameters are independently and can be unrestricted combined. Hence, it is possible to select the nearest neigbhours in 3d and apply a quadrant oriented selection (and vice versa).
The normal estimation deliver more interesting data than just the normal vector itself. Beside some statistical values (sigma0, number of used observations, ...) specially the eigenvalues of the covariance matrix can be interesting for subsequent processes. Since the computed data accrue for each point, storing all values can dramatically increase the size of the used ODM files (twice the original size or even more). Therefore, the module provides the parameter storeMetaInfo which allows setting the level of meta data that are stored with each point.
minimum: stores NormalX, NormalY, NormalZ, NormalSigma0 and the estimation method (NormalEstimationMethod) medium: stores all minimum values + the three eigenvalues (NormalEigenvalue1-3) of the covariance matrix, plane offset, number of given points (NormalPtsGiven) and number of used points (NormalPtsUsed) maximum: stores all medium values + the corresponding eigenvectors For additional details of the normal attributes see the predefined attributes of the ODM.
The orientation of the normal vector can be controlled by the parameter direction. As default the normals are oriented upwards towards the positive z-axis (NormalZ >= 0). This can lead to flipping orientations on vertical (or near vertical) surfaces (see opals::NormalsDirection for more options).
For completeness it should be mentioned that NormalSigma0 is only set if the redundancy of the adjustment is greater than zero (otherwise it is set to null). If this sigma is required by subsequent processes (like Module EchoRatio) the number of neighbours should be carefully chosen, especially, if robust estimators are used.
Within Module Normals the powerful OPALS filters can be used in two different ways. The first filter defines in which points a normal should be estimated. The second filter entry selects the points the are used for the neighbour search. If only one filter is provided, it is used for both filtering stages. Hence, it is possible to estimate normals for single echoes only but all last echoes are used as neighbouring information. Situations are imagineable where different estimators should be used for different subsets. Or a second (or third) run of Module Normals with adapted parameters is performed to compute normals for points where previous runs have failed (without changing existing results). All these issues can be handled by setting appropriate filter strings. For details see the Examples section.
Possible values: d2 ... Search based on 2D coordinates (x and y) only d3 ... Search based on full 3D coordinates (x,y and z)Defines if 2D or 3D distances should be used for the nearest neighbor search
The data used in the following example are located in the $OPALS_ROOT/demo/ directory. The example shows how to use opalsNormals including a short analysis of the results.
As a prerequisite, the ALS point cloud data must be imported into the ODM. To achieve that, change to the demo directory and type:
Now, run the following command
to perform the local plane estimation selecting 8 neighbours in an 3d neighbourhood. To avoid extrapolations the selection mode is set to quadrant.
One possiblity to check the computed normals is a visualization of the vector output, e.g. using the debugOutFile parameter. On a larger scale, however, opalsHisto is a valuable tool for similar verifications. Executing the following commands
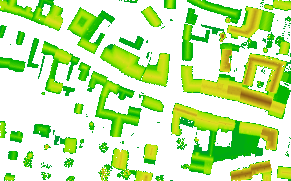
produces two histograms as shown in Figure 2. The data set covers an urban area (see Figure 3) with little degree of vegetation. This accords to the textual output from this first opalsHisto run. It can be seen that 75% of all sigma0 values are below 6 [cm]. In the histogram of the the y component of the normal vectors (right diagram in Figure 2) two interesting bumps (at position +/- 0.6) are cleary visible. Those result from the significant amount of saddle roofs with an east-west ridge.
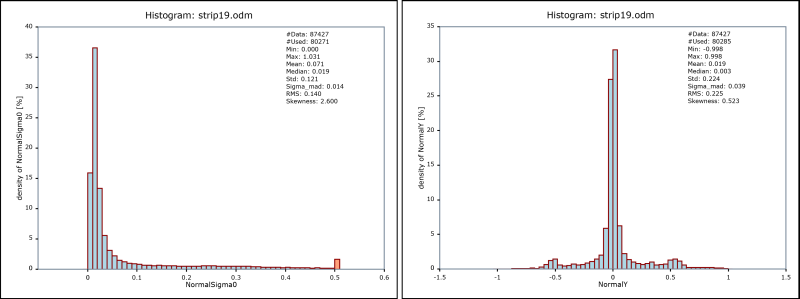
NormalSigma0) and the y component of normal vectors (right: NormalY)
1.8.17